library(calm)
library(ggplot2)
library(dplyr)
library(tidyr)
theme_set(theme_bw())
data(pati)
set.seed(2022)Fitting HeiDI to empirical data
In this demo, I fit HeiDI to some empirical data (Patitucci et al., 2016, Experiment 1). This will involve writing a function that produces model responses organized as the empirical data, and using that function for maximum likelihood estimation (MLE). We begin with a short overview of the data, then move to the model function, and finally fit the model.
The data
The data (pati) contains the responses (lever presses or
lp, and nose pokes or np) for 32 subjects (rats) across 6 blocks of
training (2 sessions per block). The animals were trained to associate
each of two levers to one of two unconditioned stimuli (pellets or
sucrose). Let’s take a look at it.
glimpse(pati)
#> Rows: 768
#> Columns: 6
#> $ subject <fct> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1…
#> $ block <dbl> 1, 2, 3, 4, 5, 6, 1, 2, 3, 4, 5, 6, 1, 2, 3, 4, 5, 6, 1, 2, 3…
#> $ lever <fct> L, L, L, L, L, L, R, R, R, R, R, R, L, L, L, L, L, L, R, R, R…
#> $ us <chr> "P", "P", "P", "P", "P", "P", "S", "S", "S", "S", "S", "S", "…
#> $ response <fct> lp, lp, lp, lp, lp, lp, lp, lp, lp, lp, lp, lp, np, np, np, n…
#> $ rpert <dbl> 0.9000, 1.5500, 3.3500, 4.1500, 4.6500, 4.3250, 0.4000, 0.162…
pati |> ggplot(aes(x = block, y = rpert, colour = us)) +
geom_line(aes(group = interaction(us, subject)), alpha = .3) +
stat_summary(geom = "line", fun = "mean", linewidth = 1) +
labs(x = "Block", y = "Responses per trial", colour = "US") +
facet_grid(~response)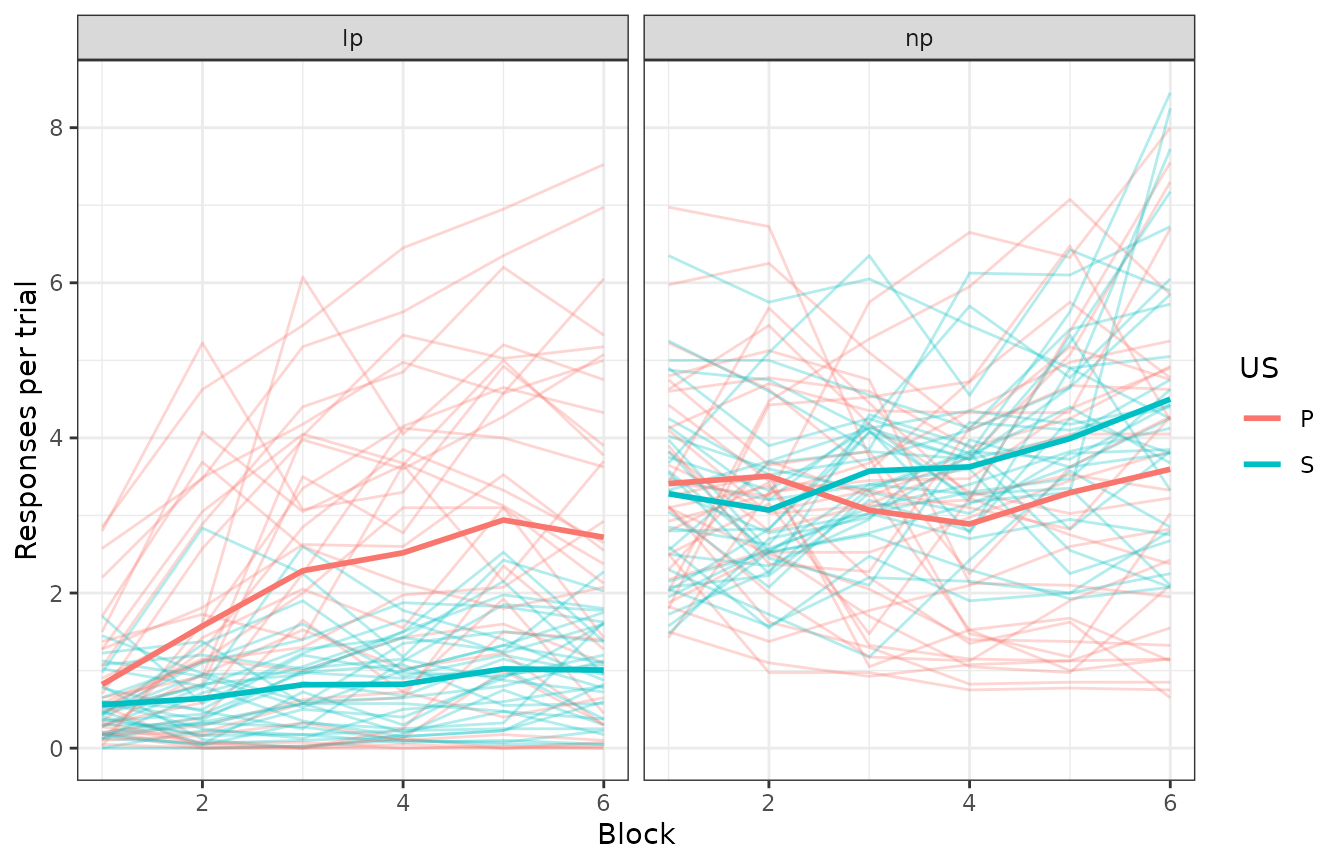
The thicker lines are group averages; the rest are individual subjects. We ignore the specific mapping between levers and USs here, because that was counterbalanced across subjects. However, the counterbalancing will end up being relevant (see ahead).
Writing the model function
The biggest hurdle in fitting the model to empirical data is to write a function that, given a vector of parameters and model arguments, generates responses that are organized as the empirical data. Let’s begin by summarizing the group data first, so we know what to aim for.
pati_summ <- pati |>
group_by(block, us, response) |>
summarise(rpert = mean(rpert), .groups = "drop")
head(pati_summ)
#> # A tibble: 6 × 4
#> block us response rpert
#> <dbl> <chr> <fct> <dbl>
#> 1 1 P lp 0.820
#> 2 1 P np 3.41
#> 3 1 S lp 0.561
#> 4 1 S np 3.28
#> 5 2 P lp 1.57
#> 6 2 P np 3.51We now prepare the arguments for the model function (as you would
pass to run_experimentexperiment.
This is no minor issue because the HeiDI is sensitive to order effects. Hence, the arguments we prepare here must reflect the behavior of the model after a “general” experimental procedure, and not the quirks of an unfortunate run of trials. Here, we simply address this issue by running several iterations of the model (with random trial orders) and averaging all models before evaluating the likelihood of the parameters.
So what do we have to design? The experiment presented by Patittuci et al. (2016) was fairly simple, and it can be reduced to the presentations of two levers, each followed by a different appetitive outcome. Here, we will assume that the two outcomes are independent from each other. We will also take some liberties with the number of trials we specify, to reduce computing time.
# The design data.frame
des_df <- data.frame(
group = c("CB1", "CB2"),
training = c(
"12L>(Pellet)/12R>(Sucrose)",
"12L>(Sucrose)/12R>(Pellet)"
),
rand_train = TRUE
)
# The parameters
# the actual parameter values don't matter,
# as our function will re-write them inside the optimizer call
parameters <- get_parameters(des_df,
model = "HD2022"
)
# The arguments
experiment <- make_experiment(des_df,
parameters = parameters, model = "HD2022",
iterations = 4
)Note we specified two counterbalancings as groups. We must reproduce
the counterbalancings in the data we are trying to fit as close as
possible. Otherwise, the optimization process might latch onto
experimentally-irrelevant variables. For example, it can be seen in
pati that there was more lever pressing whenever a lever
was paired with pellets. If we didn’t counterbalance the identities of
the levers and USs, the optimization might result in one of the levers
being less salient than the other.
We can now begin to write the model function. First, it would be a
good to see what results run_experiment returns.
exp_res <- run_experiment(experiment)
results(exp_res)
#> $as
#> group phase trial_type trial s1 block_size value model
#> <char> <char> <char> <int> <fctr> <num> <num> <char>
#> 1: CB1 training L>(Pellet) 1 L 2 0.4 HD2022
#> 2: CB1 training R>(Sucrose) 2 L 2 0.0 HD2022
#> 3: CB1 training R>(Sucrose) 3 L 2 0.0 HD2022
#> 4: CB1 training L>(Pellet) 4 L 2 0.4 HD2022
#> 5: CB1 training R>(Sucrose) 5 L 2 0.0 HD2022
#> ---
#> 340: CB2 training R>(Pellet) 10 Pellet 2 0.4 HD2022
#> 341: CB2 training L>(Sucrose) 9 R 2 0.0 HD2022
#> 342: CB2 training R>(Pellet) 10 R 2 0.4 HD2022
#> 343: CB2 training L>(Sucrose) 9 Sucrose 2 0.4 HD2022
#> 344: CB2 training R>(Pellet) 10 Sucrose 2 0.0 HD2022
#>
#> $acts
#> group phase trial_type trial s1 s2 block_size type
#> <char> <char> <char> <int> <char> <char> <num> <char>
#> 1: CB1 training L>(Pellet) 1 LPellet L 2 combvs
#> 2: CB1 training L>(Pellet) 1 LPellet Pellet 2 combvs
#> 3: CB1 training L>(Pellet) 1 LPellet R 2 combvs
#> 4: CB1 training L>(Pellet) 1 LPellet Sucrose 2 combvs
#> 5: CB1 training R>(Sucrose) 2 LPellet L 2 combvs
#> ---
#> 1268: CB2 training R>(Pellet) 10 L Sucrose 2 chainvs
#> 1269: CB2 training R>(Pellet) 10 Sucrose L 2 chainvs
#> 1270: CB2 training R>(Pellet) 10 Sucrose Pellet 2 chainvs
#> 1271: CB2 training R>(Pellet) 10 Sucrose R 2 chainvs
#> 1272: CB2 training R>(Pellet) 10 Sucrose Sucrose 2 chainvs
#> value model
#> <num> <char>
#> 1: 0 HD2022
#> 2: 0 HD2022
#> 3: 0 HD2022
#> 4: 0 HD2022
#> 5: 0 HD2022
#> ---
#> 1268: 0 HD2022
#> 1269: 0 HD2022
#> 1270: 0 HD2022
#> 1271: 0 HD2022
#> 1272: 0 HD2022
#>
#> $rs
#> group phase trial_type trial s1 s2 block_size value model
#> <char> <char> <char> <int> <char> <char> <num> <num> <char>
#> 1: CB1 training L>(Pellet) 1 L L 2 0 HD2022
#> 2: CB1 training L>(Pellet) 1 L Pellet 2 0 HD2022
#> 3: CB1 training L>(Pellet) 1 L R 2 0 HD2022
#> 4: CB1 training L>(Pellet) 1 L Sucrose 2 0 HD2022
#> 5: CB1 training L>(Pellet) 1 Pellet L 2 0 HD2022
#> ---
#> 1372: CB2 training R>(Pellet) 10 R Sucrose 2 0 HD2022
#> 1373: CB2 training R>(Pellet) 10 Sucrose L 2 0 HD2022
#> 1374: CB2 training R>(Pellet) 10 Sucrose Pellet 2 0 HD2022
#> 1375: CB2 training R>(Pellet) 10 Sucrose R 2 0 HD2022
#> 1376: CB2 training R>(Pellet) 10 Sucrose Sucrose 2 0 HD2022
#>
#> $vs
#> group phase trial_type trial s1 s2 block_size value
#> <char> <char> <char> <int> <char> <char> <num> <num>
#> 1: CB1 training L>(Pellet) 1 L L 2 0.000000
#> 2: CB1 training L>(Pellet) 1 L Pellet 2 0.000000
#> 3: CB1 training L>(Pellet) 1 L R 2 0.000000
#> 4: CB1 training L>(Pellet) 1 L Sucrose 2 0.000000
#> 5: CB1 training L>(Pellet) 1 Pellet L 2 0.000000
#> ---
#> 1372: CB2 training R>(Pellet) 10 R Sucrose 2 0.000000
#> 1373: CB2 training R>(Pellet) 10 Sucrose L 2 0.368896
#> 1374: CB2 training R>(Pellet) 10 Sucrose Pellet 2 0.000000
#> 1375: CB2 training R>(Pellet) 10 Sucrose R 2 0.000000
#> 1376: CB2 training R>(Pellet) 10 Sucrose Sucrose 2 0.000000
#> model
#> <char>
#> 1: HD2022
#> 2: HD2022
#> 3: HD2022
#> 4: HD2022
#> 5: HD2022
#> ---
#> 1372: HD2022
#> 1373: HD2022
#> 1374: HD2022
#> 1375: HD2022
#> 1376: HD2022Although the run_experiment function returns an S4 class
with many things, we only care about one of them: rs (the
model responses). With them, we can write our model function.
my_model_function <- function(parameters, experiment) {
# manipulating parameters
new_parameters <- parameters(experiment)[[1]]
new_parameters$alphas[] <- parameters
parameters(experiment) <- new_parameters # note parameters method
# running the model and selecting rs
exp_res <- run_experiment(experiment)
# summarizing the model
rs <- results(exp_res)$rs |>
filter(s2 %in% c("Pellet", "Sucrose")) |>
mutate(
response = ifelse(s1 %in% c("Pellet", "Sucrose"), "np", "lp"),
block = ceiling(trial / 4)
) |>
rowwise() |>
# note this filter below;
# we do not allow lever presses if the lever was not presented on the trial
filter(response == "np" | (response == "lp" & grepl(s1, trial_type))) |>
mutate(us = ifelse(grepl("Pellet", trial_type), "P", "S")) |>
group_by(block, us, response) |>
summarise(value = mean(value), .groups = "drop")
rs$value
}Let’s dissect the function above in its three parts.
We put
parameters(the optimizer parameters) into the experiment using theparametersmethod.We run the model and select the relevant information (rs).
We summarise the model responses and return them.1
Let’s see the function in action.
my_model_function(c(.1, .2, .4, .3), experiment = experiment)
#> [1] 0.009200000 0.003028571 0.012075000 0.005769643 0.027451634 0.010299086
#> [7] 0.046803321 0.021698787 0.048681560 0.016592848 0.052716098 0.029575459
#> [13] 0.050783660 0.019358818 0.066233126 0.036222556 0.055000834 0.021867550
#> [19] 0.070767634 0.040360835 0.057311961 0.023442829 0.073063348 0.042882258The order of the empirical data and model responses must match. I cannot emphasize this point enough: there is nothing within the fit function that checks or reorders the data for you. You are the sole responsible for making sure both of these pieces of data are in the same order. A simple way would be to print the model results before the return (see above). Once we have made sure everything is looking good, we can fit the model.
Fitting the model
We fit models using the fit_model function. This
function requires 4 arguments:
- The (empirical) data
- A model function
- The arguments with which to run the model function.
- The optimizer options.
We have done a great job taking care of the first three, so let’s tackle the last.
my_optimizer_opts <- get_optimizer_opts(
model_pars = names(parameters$alphas),
optimizer = "ga",
ll = c(0, 0, 0, 0),
ul = c(1, 1, 1, 1),
family = "normal"
)
my_optimizer_opts
#> $model_pars
#> [1] "L" "Pellet" "R" "Sucrose"
#>
#> $optimizer
#> [1] "ga"
#>
#> $family
#> [1] "normal"
#>
#> $family_pars
#> [1] "normal_scale"
#>
#> $all_pars
#> [1] "L" "Pellet" "R" "Sucrose" "normal_scale"
#>
#> $initial_pars
#> [1] NA NA NA NA
#>
#> $ll
#> L Pellet R Sucrose normal_scale
#> 0 0 0 0 0
#>
#> $ul
#> L Pellet R Sucrose normal_scale
#> 1 1 1 1 100
#>
#> $verbose
#> [1] FALSEThe get_optimizer_opts function returns many things:
- model_pars: The name of the model parameters. Here, the name of the alphas for each stimuli.
- ll and ul: The lower and upper limits for the parameter search. Consider shrinking these to speed up the process.
- optimizer: The numerical optimization technique we wish to use during MLE estimation.
- family: The family distribution we assume for our model. In practice, what you request here will be used to determine the link function to transform model responses, and the likelihood function used in the objective function. The normal family here does nothing fancy to the model responses, and will estimate an extra parameter, scale, which scales the model responses into the scale of the empirical data. When it comes to likelihood functions, this family will use the normal density of the data and model differences.
- family_pars: The family-specific parameter being estimated alongside salience parameters.
- verbose: Whether to print parameters and objective function values as we optimize.
You are free to modify these; just make sure the structure of the
list returned by get_optimizer_opts remains the same.
We can also pass extra parameters to the optimizer call we are using
(e.g., the par argument for optim, or
parallel for ga). Here, we fit the model in
parallel with ga, and for only 10 iterations.
And with that, we can fit the model! (be patient if you are following along)
the_fit <- fit_model(pati_summ$rpert,
model_function = my_model_function,
experiment = experiment,
optimizer_options = my_optimizer_opts,
maxiter = 10,
parallel = TRUE
)The fit_model function returns a lot of information to
track what we put in and what we got out. However, typing the model in
the console will show the MLE parameters we obtained this time and their
negative log likelihood, given the data:
the_fit
#> Calm model fit:
#> Parameters:
#> L Pellet R Sucrose normal_scale
#> 0.1576156 0.8031082 0.2654031 0.6415039 25.9897647
#>
#> nLogLik:
#> 38.61801That’s good and all, but how well does a model run with those
parameters “visually” fit the data? We can obtain the predictions from
the model via the predict function.
pati_summ$prediction <- predict(the_fit, experiment = experiment)
pati_summ |>
rename("data" = "rpert") |>
pivot_longer(
cols = c("prediction", "data"),
names_to = "type",
values_to = "value"
) |>
ggplot(ggplot2::aes(x = block, y = value, colour = us, linetype = type)) +
geom_line() +
theme_bw() +
facet_grid(us ~ response)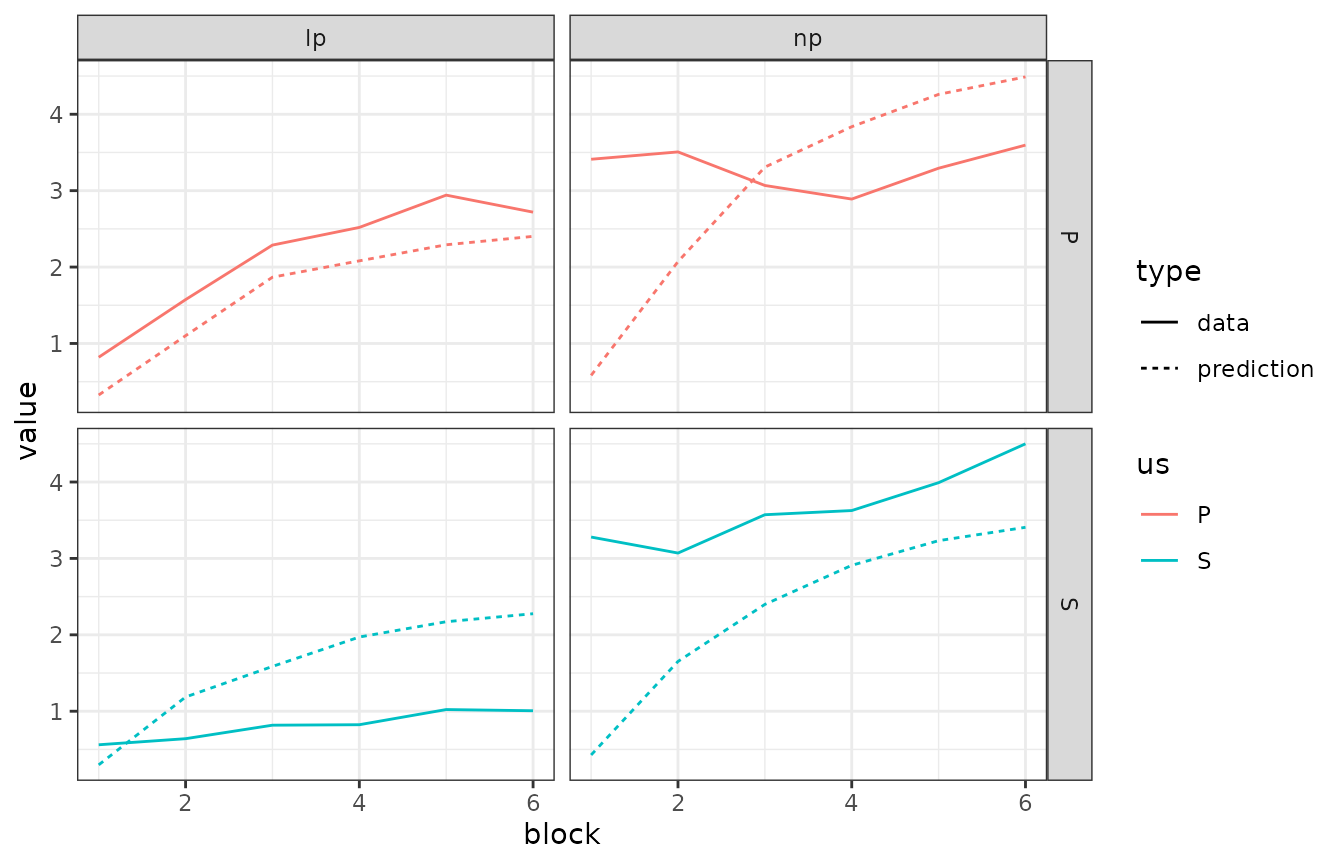
This looks pretty good! Save from some blatant misfits, of course. Now you know everything you need to fit calm to your empirical data. Go forth!